Inferring Traffic Counts from Network Centrality

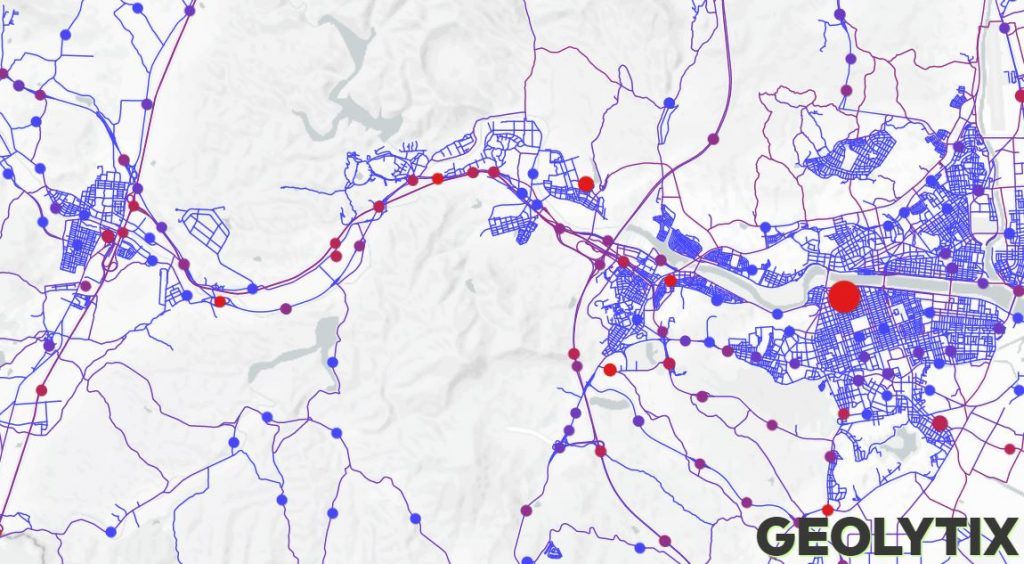
The client operated in South Korea, so we had some data challenges ahead! In the UK we produce and update a road and traffic dataset that we can use for this kind of work, however we didn’t yet have anything for South Korea. So, the aim was to build a network with a modelled value for traffic count for every major road in the country of operation.

For the baseline road network we started with a pull of the data available for South Korea from Open Street Map. We processed this to extract the Roads as a reputable network using an open source converter. In order to validate our modelled traffic values we needed some actual traffic counts. Luke in our Tokyo office managed to come across this exact dataset from Topis. With all of this we were ready to start modelling!

In order to infer traffic flow between our known survey points we utilised the routability of the road network and exploited the power of graph theory calculations. Graph theory is the study of a network of related objects where vertices (points) are related to each other by edges (lines).

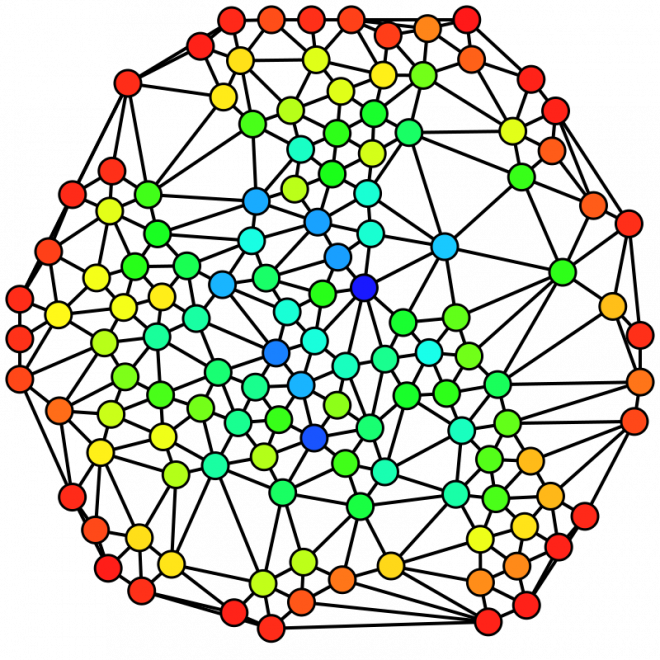
Graphs are used in a diverse number of fields, particularly those incorporating complex systems such as social networks, linguistics, and chemistry. In our example the roads are a network of connected junctions. Knowing the distance in real space between these junctions gives the edges a weight, and if the road is one way or not gives the edges a direction.

This gives us a weighted, directed network which we can start to do some pretty cool things with.

Graph algorithms are used in several ways, for things like community detection (how do the vertices group together, do they cluster?), shortest path finding, or measuring connectedness. This connectedness measurements fall under the bracket of centrality algorithms. This was our golden ticket to inferring traffic counts on our network.

The algorithm we used is called betweenness centrality, it is a measure of the importance of each node on the flow through the network. It effectively gives a score of influence to a node by assessing how many times it is used in a shortest path between two other nodes. In other practices it can be used in social sciences looking into who is the most important person in a management team to the flow of information. For us it gives a measure of how utilised a road is based on the huge number of different paths that can be made through the network.

If a road is going to be used by more journeys, we can infer that there are probably going to be more cars on it.

Because of the scale of the network (we had 1,180,746 roads in South Korea) we were going to need some horse power, so we started up a Google Cloud Dataproc machine to get Hadoop to do some of the heavy lifting. We wrote a script which would calculate the betweenness of the edges based on shortest paths within a certain depth of the vertices. In theory, betweenness is built from calculations of every possible shortest path, however in reality this is too much computation, and after a certain threshold you gain no more insight by calculating more routes.

Once we’d assigned the surveyed traffic counts to their nearest roads, and applied relative urbanities to the network we used a delta difference approach to then smooth these traffic counts across the network.
With some tweaking we were happy with our outputs and we then incorporated this into our network blueprint to identify opportunities for new drive-thrus.

We learnt a lot from this project, this was a great case study for Hadoop and graph algorithms. We are excited the methodology allows us to build this data anywhere in the world, and we are actively experimenting with ways we can include insights from graph theory elsewhere in our projects.